
Последна редакция на тази статия: 6 юли 2005 г.
Тази статия е едно съществено допълнение и продължение на основната идея, изложена по-рано в [Pet02a1].
Всъщност, би било най-добре, ако [Pet02a1], настоящата работа и предстоящата публикация [Pet02a3] бъдат четени в бърза последователност. Тези три работи могат да бъдат разглеждани като образуващи нещо като "триада от статии", които по същество засягат една и съща тема, но само че с постепенно увеличаване на дълбочината на изложение и необходимото ниво на разбиране, което се изисква от читателя.
Докато ние сме сигурни, че първата статия от "триадата" [Pet02a1] ще бъде възприета лесно от повечето читатели като един провокиращ ума аргумент в подкрепа на идеята за "Вселената като компютър", нашето предварително очакване е, че мнозина могат да имат съществени трудности да схванат далеч по-дълбоките и разнообразни идеи зад настоящата работа.
Колкото до [Pet02a3], нашата надежда е, че поне някои наши читатели ще бъдат способни да я разберат. Наистина, това, което ние се каним да изложим в последната статия от триадата, ще бъде дотолкова "извън всякаква аналогия", известна ни от коя да е друга научна област, или просто "неописуемо", че то може да изисква цялостна ревизия в мисленето на читателя, за да може той (или тя) да бъде способен да схване идеята, дори частично.
За да резюмираме накратко нашия план, бихме могли да кажем, че основната идея на [Pet02a1] беше да убеди читателя, че Вселената може би наистина е някакъв вид изчислително устройство, или, казано другояче, че най-малкото има някаква определена полза в това да гледаме на Вселената така, сякаш тя е компютър.
Идеята на настоящата работа е да покаже, че нашата Вселена е не просто "някакъв вид изчислителна машина", а именно един конкретен модел за изчисление, известен като "клетъчен автомат". Идеята за това, че Вселената е клетъчен автомат, е известна като "Тезис на Цузе-Фредкин".
И, най-накрая, вярвате или не, идеята на [Pet02a3] е да покаже, че Тезисът на Цузе-Фредкин сам по себе си, в някакъв смисъл, е самодостатъчно твърдение, т.е. всичко, от което се нуждаем, за да изведем (математически) точната форма на клетъчния автомат, за който се предполага, че е изоморфен на нашата Вселена, е самият Тезис на Цузе-Фредкин, и... нищо друго!1
Но, за момента, нека да се върнем към нашите исторически бележки от [Pet02a1] и забележителния период от време, когато цялостната идея зад т.нар. "Тезис на Чърч-Тюринг" възниква.
Трудно е да се повярва, но повечето от тези извънредно важни понятия и резултати се "случват" в рамките на по-малко от едно десетилетие, когато мнозина различни изследователи стигат до (по същество) едни и същи идеи независимо един от друг. И това златно десетилетие започва да формира наново цялостния начин, по който гледаме на нещата в науката като цяло, разпростиращ се от философията и квантовата физика до математиката и теоретичната информатика.
"Не е нито веднъж, нито дваж, а безчет пъти, когато едни и същи идеи се появяват на този свят."
(Аристотел, "За Божественото")
"Ние с такава готовност допускаме, че откривателството, също както виждането или докосването, би трябвало да бъдe недвусмислено приписвано на един индивид и един определен момент от време. Но последното е винаги невъзможно, а и първото често също не е. [...] Откривателството [...] включва също и момента на признание, че нещо съществува и какво всъщност е то."
(Томас Кун, "Структура на научната революция", второ издание, 1970)
Тридесетте години на миналия век трябва да са били едно наистина забележително време...

|
Тази теорема дава един критерий за това дали даден граф може да бъде начертан в две или три измерения без самопресичане на ребрата (вж. Фиг. 1). Даже от днешна перспектива това все още остава един важен резултат, който лежи в основите на съвременната Теория на Графите.
(Това, което е по-малко известно, обаче, е че тази теорема е била доказана също по-рано от Понтрягин (18) и по-късно от Франк и Смит (1930) — за детайлна история на теоремата вж. [KQS85]).

Фигура 1: Съгласно теоремата на Куратовски, всеки граф, който не може да бъде изобразен в равнината без самопресичане на ребрата си съдържа като подграф т. нар. "пълен граф K5" или "графа на услугите K3,3". Графът K5 се състои от пет взаимно свързани върха; графът K3,3 съдържа две групи от по 3 върха всяка, където всеки връх от някоя група е свързан с всички върхове, принадлежащи на другата група.Тази теорема ни дава едно необходимо и достатъчно условие, което ни позволява да различаваме двумерните от тримерните графи.
Връзката между това, което днес е известно като "Теорема на Куратовски" и клетъчните автомати, ще бъде разгледана по-късно в Параграф 7.

|
Тази работа е добре позната заради две от нейните теореми, сега известни като "Теореми на Гьодел за непълнота".
(Резултатите на Гьодел, обаче, са били доказани по-рано — но не и публикувани — от Зермело и Пост.)
Макар и до известна степен упростено, бихме могли да кажем, че първата Теорема за непълнота твърди, че във всяка достатъчно сложна аксиоматична система, която позволява да се извършват основни аритметични действия над нея, може да бъде конструирано твърдение, което:
(1) не може да бъде доказано, че е вярно, нито пък, че е невярно, в рамките на тази система;
или
(2) може да бъде доказано, че е едновременно вярно и невярно.
В първия случай казваме, че аксиоматичната система е "непълна"; във втория случай казваме, че тя е "противоречива". Твърдение от горния вид наричаме "неразрешимо" в рамките на тази система.
Втората теорема за непълнота твърди, че в рамките на една достатъчно сложна и непротиворечива аксиоматична система не може да бъде доказана нейната собствена непротиворечивост. Важността на теоремите на Гьодел за непълнота във връзка с тезиса на Цузе-Фредкин ще бъде разгледана подробно по-късно в [Pet02i].
В периода 16 г. са били публикувани множество важни статии2:
Растящият интерес към проблема за намиране на строга дефиниция на интуитивното понятие за "математическа функция" води до появата на понятия като "ламбда-дефинируеми функции", въведени от Алонзо Чърч [Chu32, Chu36b] и Стивън Клийни [Kle35], a също на понятието за "рекурсивни функции", изучавани от Жак Хербранд [Her32] и Курт Гьодел [Goe34].
Тези два формализма описват едно и също множество от функции, така, както е било доказано в случая за функции над положителни цели числа от Чърч [Chu36a] и Клийни [Kle36].

|
Машините на Тюринг са абстрактни модели за извършване на изчисление, дефинирани от Тюринг с цел да се даде математически прецизна дефиниция на понятието "алгоритъм" или "механична процедура".
Една машина на Тюринг може да бъде конструирана под формата на механично устройство, което се състои от (вж. Фиг. 2):
Забележете, че всяка отделна част от машината е крайна, но ние разполагаме с потенциално безкрайно количество от лента, което ни дава неограничен запас от пространство за съхранение на информация (неограничена "външна памет").
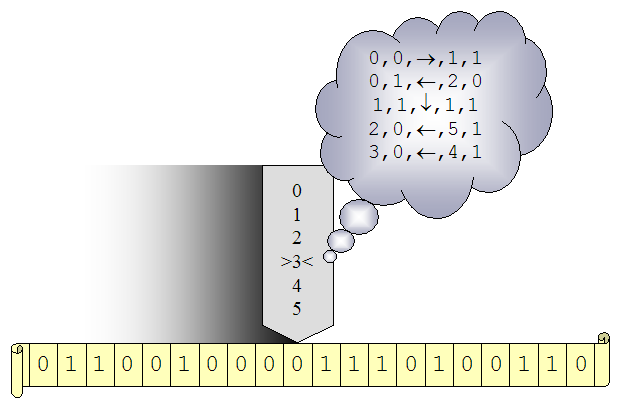
Фигура 2: Теоретичен модел на изчисление, описан от Алън Тюринг през 1936 г., известен като "Машина на Тюринг".Една машина на Тюринг се състои от: безкрайна лента, която може да съхранявя символи от някаква крайна азбука; глава, която може да чете и пише символи върху лентата и (евентуално) да се придвижва наляво или надясно до следващия символ от лентата; регистър на състоянията, който може да заема крайно множество от състояния, и множество от инструкции (обикновено представено под формата на таблица), което се състои от команди от типа:
"ако текущия <символ>, прочетен от лентата е '0' и <състоянието на регистъра> е '3', то запиши '1' върху лентата, придвижи главата 'наляво' и промени <състоянието на регистъра> на '4' ", и т.н.
Ако не съществува инструкция какво да се прави за някаква комбинация от <текущ символ, състояние на регистъра>, то тогава машината на Тюринг спира работа и онова, което е записано върху лентата, се приема за резултат от нейната работа.
(За да видите Машината на Тюринг в действие, моля щракнете с левия бутон на мишката върху фигурата!)
Друго важно понятие е понятието за т.нар. "универсална Машина на Тюринг" ("universal Turing machine", съкр. УМТ). Една универсална машина на Тюринг е способна да симулира ("емулира") работата на коя да е друга машина на Тюринг и, както Тюринг доказва в своята работа, такива универсални машини наистина съществуват.
Някъде през 1936-37 г. възниква и идеята за т.нар. "Тезис на Чърч-Тюринг" (наричан понякога и "Тезис на Чърч-Тюринг-Пост"), и това понятие е било почти едновременно признато от редица водещи изследователи като строго математическо описание на интуитивното понятие за "математическа функция", "алгоритъм", или "изчисление".
В своята най-обща форма, тезисът на Чърч-Тюринг твърди, че всяко "ефективно изчисление" или "алгоритъм" може да бъде извършвано от универсална машина на Тюринг. Тезисът може да бъде перифразиран още и ако кажем, че понятието за "ефективен" или "механичен" метод в логиката и математиката като цяло се покрива напълно с понятието за изчисление върху машина на Тюринг.
Любопитно е да се отбележи, че Алонзо Чърч публикува своята работа [Chu36b] няколко месеца преди появата на [Tur36], но той използвал понятията за рекурсивни функции и ламбда-дефинируеми функции, за да опише формално понятието за "ефективното изчисление". Веднага, след като научава за работата на Чърч, Тюринг доказва формално, че неговите "машини на Тюринг" фактически описват същото множество от функции [Tur36].
Оттогава множество други формализми за описание на "ефективното изчисление" са били предложени, такива като "регистрови машини", "системи на Пост", "комбинатори", "алгоритми на Марков" [Mar54], и др. Тъй като за всички тези системи е било доказано, че всъщност описват същото множество от функции, сега е общоприето да се смята, че тезисът на Чърч-Тюринг е верен.
Заедно с тази посока на научно развитие, още една интересна серия от събития има своите корени през същия период от време...

|
Възможността да попадне в групата на първите компютърни програмисти и разработчици на съвременен хардуер формира у Фредкин един твърде нетрадиционен начин на мислене, който го отличава значително от общоприетите академични норми на разсъждение и поведение в науката изобщо. При все това, обаче, изглежда личността на Фредкин трябва да е била достатъчно ярка, за да може той да стане професор по информатика в MIT през шестдесетте години, при това без да има завършена диплома за висше образование.
Фредкин има възможността да сподели някои от многобройните си идеи с Ричард Фейнман, нобелев лауреат по физика, един от основоположниците на съвременната квантова механика. Животът и идеите на Фредкин са описани по неподражаем начин от Робърт Райт в [Wri88a, Wri88b].
Сред многобройните идеи на Фредкин обаче има една такава, която го прави особено популярен и, в зависимост от източника, силно обожаван или отричан.
Фредкин е единият от авторите на невероятната идея, че нашата Вселена е клетъчен автомат (cellular automaton, съкр. КА).
Клетъчните автомати са абстрактни математически модели за изчисление които, за разлика от машините на Тюринг, оперират не последователно, а при пълен паралелизъм на опрерациите при извършване на изчисление. Ако за машините на Тюринг може да се каже, че са праобраз на съвременните последователни компютри, то за клетъчните автомати може да се заяви, при това без преувеличение, че те са не просто модел на съвременните паралелни суперкомпютри, а са все още нереализирана мечта или "недостигнат идеал" за паралелните машини на бъдещето.
По своята същност, клетъчните автомати могат да бъдат описани най-кратко като безкрайно множество от паралелни процесори, разположени еднородно в пространството под формата на кристална решетка.
Всеки такъв "процесор" (наречен "клетка") е всъщност един краен автомат (Finite State Machine, съкр. FSM), който оперира, като обменя "сигнали" с процесорите, разположени в близост до него, използвайки крайно множество от вътрешни състояния и една-единствена локална детерминистична функция, еднаква за всички процесори, наречена "правило". Важно е също да се отбележи, че промяната на състоянията на всички процесори/клетки от клетъчния автомат се извършва едновременно — в един "миг" от време — който наричаме "времева стъпка" или "такт".
Според своите собствени спомени, Фрекин достига до идеята, че Вселената всъщност е клетъчен автомат, някъде през 1960 г. Тази негова идея, обаче, остава непубликувана до 1971 г., когато Мартин Гарднър я съобщава на страниците на сп. "Сайънтифик Америкън" [Gar71] в една поредица от статии, посветени на играта "Живот" ("Life").
Самата игра "Живот", едно хрумване на английския математик Джон Конуей, всъщност не е нищо друго освен клетъчен автомат върху безкрайна двумерна квадратна решетка (вж. Фиг. 3). И макар Теория на клетъчните автомати да има вече дълга история, тази "игра" и до ден днешен вероятно си остава най-популярният и добре изследван клетъчен автомат изобщо.
Фигура 3: Играта "Живот", измислена от Джон Конуей през 1970 г. Играта се играе върху безкрайна двумерна решетка. Всяко квадратче, или "клетка", може да бъде "живо" (черно) или "мъртво" (бяло). Правилата на играта "Живот" са възхитително прости:
- Ако клетката е "мъртва" и има точно три "живи" съседа (от общо осем), то тя става "жива" при следващото поколение;
- Ако клетката е "жива" и има 2 или 3 "живи" съседа, тя оцелява (остава жива) за следващото поколение;
- Във всички останали случаи клетката умира.
"Живот" е достатъчно сложна игра, за да може да породи много динамични и красиви клетъчни структури. Трите често срещани конфигурации, показани по-горе, са наречени "блок" (a), "семафор" (b) и "глейдер" (c); това са примери за неподвижна, периодична и движеща се конфигурация, съответно.
(Щракнете с левия бутон на мишката за Java анимация!)

|
Покойният вече Цузе е бил гениален немски инженер, който сега е признат за изобретател на първия програмируем компютър и първия език за програмиране от високо ниво. Любопитно е да се отбележи, че Конрад Цузе разработва действащ модел на своя компютър практически по същото време, когато Алън Тюринг стига до идеята за "машина на Тюринг". През 1936 г. Цузе дори подава документ за патент [Zus36], който той в крайна сметка не получава. Изправен пред дилемата дали да се бори за патент — нещо, което би могло да бъде доста скъпо — или да създаде практически действащо устройство, Цузе решава в крайна сметка да се посвети на второто.
И, разбира се, Цузе разработва своето изчислително устройство в пълно неведение за идеите на Тюринг, напълно независимо от последния.

|
Научната работа на Попър е била повлияна от изучаването на Теория на относителността на Алберт Айнщайн, която първият използва като пример за разликата между действително научната и псевдо-научната теории. Съгласно гледната точка на Попър, разликата е, че теории като тази на Айнщайн могат да бъдат лесно и веднага отхвърлени от прости експерименти, ако са неверни. Този критерий за "провал" ("фалсификация") и практиката да се използват експерименти не да се провери, а да се отхвърли дадена научна теория, са крайъгълен камък на истинската наука според Попър, в противоположност на общоприетото схващане през това време (предложено от Франсис Бейкън), че науката се основава на разсъждение по индукция и експериментална проверка ("верификация").

|
"Може даже да се измислят доста абсурдни случаи. Котка е затворена в стоманена камера, заедно със следното дяволско устройство (което трябва да бъде защитено от директна намеса от страна на котката): в Гайгеров брояч има съвсем малко радиоктивно вещество, толкова малко, че може би в течението на един час един от атомите се разпада, но също така, с равна вероятност, може би нито един; ако това се случи, броячът се задейства и посредством някакъв механизъм освобождава чук, който разбива малка колба с циановодородна киселина. Ако сме оставили цялата тази система без намеса за един час, бихме могли да кажем, че котката е все още жива ако междувременно нито един атом не се е разпаднал. Първият разпад на атом би отровил котката. Пси функцията за цялата система би изразила това като че ли имаме в камерата живата и мъртва котка (простете за израза) в смесено или "зацапано" състояние в равни части.
Характерното за такива случаи е, че неопределеността, първоначално ограничена в областта на атомите, се трансформира в макроскопска неопределеност, която след това може да бъде разрешена посредством директно наблюдение. Това ни предпазва от възможността толкова наивно да приемем за валиден "зацапания" ("замъгления") модел като представящ реалността. Сам по себе си той не би включвал нещо неясно или противоречиво. Има разлика между развалената (или нефокусирана) фотография и между снимка на облаци и мъгливи брегове."
Бързаме да успокоим читателя, че ако той се е почувствал неуютно от приведения цитат и казаното по-горе му се е сторило донякъде мъгливо, то това не е случайно. С известна доза чувство за хумор можем да кажем само, че изглежда самият Шрьодингер се е намирал в някакво "зацапано" или "размазано" състояние, когато е писал въпросния пасаж.
Въобще, такова "неопределено" състояние, където авторът (от една страна) сякаш се опитва да се надсмее над нещо, а от друга — някак си, все пак, в крайна сметка иска да го оправдае, е характерно за повечето физици, които се занимават с квантова механика. Шрьодингер, който е един от нейните основоположници, в този смисъл не прави изключение.
(Както Ричард Файнман по-късно ще признае: "Ако някой ви каже, че разбира квантовата механика, не му вярвайте! Всъщност, никой не я разбира...")
Все пак, парадоксът с котката на Шрьодингер е несъмнено едно добро попадение, разкриващо абсурдността на "новите" (за времето си) идеи във физиката. Наистина, къде минава границата между неопределеността, характерна (според квантовата механика) за микросвета, и макроскопската определеност, която сме свикнали да очакваме от нашия ежедневен опит?

|
Не би било преувеличено да се каже, че парадоксът на Айнщайн-Подолски-Розен е бил (и все още е) считан от мнозина водещи физици като основен проблем във връзка с приемането на тезиса на Цузе-Фредкин; факт е, че именно EPR е основната причина идеята за "Вселената като клетъчен автомат" да не бъде приета сериозно. Наместо това, по-късно (през деветдесетте години) идеята за т.нар. "квантово изчисление" беше енергично предлагана и разработвана.
Наистина, периодът 17 г. е бил едно забележително за науката време... Един златен период, който слага началото на голяма мисловна революция и трасира научното развитие до самия край на двадесети век.
За разлика от тезиса на Чърч-Тюринг, който е бил лесно приет сред всички основни научни кръгове през средата на 30-те години (по-специално, сред математиците и пионерите на възникващата тогава теоретична компютърна наука), тезисът на Цузе-Фредкин е имал по-малко късмет [Pet02a1].
Факт е, че дори днес тезисът на Цузе-Фредкин си остава до голяма степен публично неизвестен и неприет.
В нашата работа [Pet02a1] ние предложихме един сравнително прост, но достатъчно убедителен аргумент в подкрепа на тезиса на Цузе-Фредкин.
Един внимателен читател на [Pet02a1], обаче, би трябвало да забележи, че от нашия агрумент ни най-малко не следва, че Вселената е именно клетъчен автомат, а по-скоро следва, че нашата Вселена е някакъв вид изчислително устройство.
В настоящата статия ние ще запълним този пропуск, разглеждайки всички основни контрааргументи, които са били предлагани въобще някога срещу тезиса на Цузе-Фредкин и, в защита на тезиса, ние ще дадем конкретно обяснение на всеки един от тях.
Както ще видим по-долу, до известна степен изненадаващо е, че докато възраженията срещу тезиса на Цузе-Фредкин могат да бъдат доста различни по своята природа и произход, всички те могат да бъдат разделени на две големи групи в зависимост от обясненията, които могат да им бъдат дадени.
А всички обяснения, които могат да бъдат дадени в защита на идеята за "Вселената като клетъчен автомат", могат да бъдат разделени на следните две големи групи:
(B) Обяснения, които използват новата идея, че тезисът на Чърч-Тюринг е всъщност една недоразвита (т.е. до известна степен "незряла") форма на тезиса на Цузе-Фредкин — така, както се предлага в настоящата работа.
Малко или много е неочаквано, че повечето от добре известните контрааргументи, предлагани срещу тезиса на Цузе-Фредкин, всъщност попадат в първата категория (A). Например, често излаганата и безкрайно повтаряна теза, че Вселената е всъщност фундаментално непрекъсната и вероятностна по своята същност (но не дискретна и детерминистична) е лесно оборима в рамките само на тезиса на Чърч-Тюринг.
Понятия като "(актуална) безкрайност", "непрекъснатост", "вероятност", различни форми на "дуализъм" (да вземем за пример т.нар. "корпускулярно-вълнови дуализъм"), а също различни форми на "многозначност" и "мултизъм" (мислете си за т.нар. "Интерпретация за многото светове" — "Many Worlds Interpretation", съкр. MWI — сега модерна в квантовата физика) са били приемани за "даденост" от съвременните физици за десетилетия. Но както ще видим по-долу, оказва се, че всички тези понятия са просто "мисловни чудовища", които лесно се опровергават и "разпръсват във въздуха" — при това, за да ги опровергаем, ние ще си послужим с един-единствен aргумент: тезисът на Чърч-Тюринг!
Една специална категория от проблеми, обикновено повдигани в математическите среди, включва Втората теорема на Гьодел за непълнота. Както ние ще видим по-късно в настоящата работа и по-детайлно в [Pet02i], всички контраарументи срещу тезиса на Цузе-Фредкин (и всяка идея за добре дефинирана "Теория за всичко съществуващо") всъщност отново са лесно защитими в рамките само на тезиса на Чърч-Тюринг.
Сред контрааргументите от втория клас (такива, които не могат да бъдат защитени, използвайки тезиса на Чърч-Тюринг) специално място следва да бъде отредено на възраженията, свързани с EPR, теоремата на Бел [Bel64] и концепцията за "квантово изчисление". Факт е, че всички останали възражения може да не бъдат считани за достатъчно сериозни, но този спорен въпрос сам по себе си е всъщност основната причина тезисът на Цузе-Фредкин да не бъде широко приет във физичните среди.
Докато сериозното разглеждане на този проблем лежи отвъд ограничените рамки на настоящата статия, все пак, тук ние ще изложим накратко нашата основна идея, представена в далеч по-големи детайли в [Pet02m].
За да разрешим този проблем, ще се наложи да засегнем също някои други проблеми от общата Теория на клетъчните автомати, които ще бъдат въведени тук и представени по-късно като "проблем за емулацията" [Pet02g] и "проблем за синхронизацията" [Pet02f].
Например, добре известно е, че някои "интуитивни" задачи, внушавани ни от физиката, са трудно решими с помощта на клетъчни автомати. От всички такива задачи вероятно все още с най-голяма известност се ползва проблемът за демонстриране на кръгово (или сферично) "разпространение на вълни" в рамките на двумерен (съответно, тримерен) клетъчен автомат (вж. Фиг. 4 и Фиг. 5).
Фигура 4: Демонстрация на кръгово разпространение на вълни върху двумерем клетъчен автомат.Началната конфигурация се състои от 7 долепени една до друга непразни клетки. Използваното правило е B3/S01234, т.е. нова клетка се "ражда" (от англ.: "Born"), когато празна клетка има точно три съседа, и клетка "оцелява" (от англ.: "Survives") за следващото поколение, ако има 0, 1, 2, 3 или 4 "живи" съседа.
Това правило е открито от Норман Пакард и Стивън Волфрам.
(Щракнете върху фигурата с левия бутон на мишката за Java анимация)
Фигура 5: Демонстрация на сферично разпространение на вълни в тримерен клетъчен автомат.Графика и кратък филм от Джоул Добржелевски. (За да видите филма, щракнете върху фигурата с левия бутон на мишката)
Решението на тази задача загатва идеята, че има някакъв много изтънчен проблем с дефиницията на понятието за "изчисление", който не е бил "уловен" от класическата дефиниция за изчисление върху универсална машина на Тюринг. И, следователно, универсалните машини на Тюринг следва да бъдат изместени от друг, по-съвършен модел за изчисление.
Този именно модел е изчисление върху тримерни универсални клетъчни автомати. Както ще видим по-късно в настоящата работа, изчислението върху тримерни универсални клетъчни автомати има някои определени предимства пред изчисление, извършвано върху последователни машини, каквато е и универсалната машина на Тюринг.
Както е добре известно, универсалните машини на Тюринг могат да бъдат смятани за (по същество) едномерни универсални клетъчни автомати [Gut96]. Но, оказва се, че нито един едномерен универсален клетъчен автомат не е в състояние да реши задачата за "разпространение на двумерни кръгови вълни" толкова бързо, колкото това би могло да бъде пресметнато върху двумерен универсален клетъчен автомат.
По подобен начин, оказва се, че е емулацията на "равномерно разпространяващи се сферични вълни" може да бъде постигната (със същата скорост) само върху тримерни универсални клетъчни автомати, но не и върху клетъчни автомати от по-ниска размерност (т.е. при едномерни или двумерни клетъчни автомати подобна "емулация" е възможна само с условното "затихване на вълната" във времето при нейното разпространение в пространството, или "убиване на скоростта" й с течение на времето).
Такава е именно и същността на т.нар. "проблем за емулацията" [Pet02g]; това именно ни води и до новата идея да се замени класическия тезис на Чърч-Тюринг (т.е. тезиса за изчисление върху универсална машина на Тюринг, която по същество е едномерен универсален автомат) с новия тезис на Фредкин-Петров (по същество, тезис за изчисление върху универсален тримерен клетъчен автомат), така както ще бъде представен по-долу в параграф 7.
Проблемът за конструиране на физически реализируeми клетъчно-автоматни системи, които работят при пълен паралелизъм, ще бъде представен като "проблем за синхронизацията". Оказва се, че клетъчните автомати — независимо от тяхната размерност — са не просто абстрактни математически модели за изчисление, но също реални физически устройства, които могат да бъдат построени по принцип в практиката, при това с използването само на механични части [Pet02f].
В последното се заключава именно и нашият аргумент срещу идеята за "квантово изчисление": наистина, ако всички клетъчни автомати са физически реализируеми механични устройства, които при това могат да демонстрират и EPR ефекти [Pet02m], то тогава за класа на "квантовите изчислителни устройства" остава... празното множество!
С други думи: "квантовото изчисление" е една илюзия.
Няма "квантово изчисление" не защото има "някои технологични трудности" при реализацията на работещи и практически използваеми квантово-механични компютри (както напоследък се опитват да ни обяснят своите резултати неговите поддръжници), а просто защото подобни парадоксални на пръв поглед ефекти, за които се смяташе, че могат да бъдат получени само с използването на "квантово-механични" системи, всъщност могат да бъдат получени и в... напълно механични (!) системи.
Като заявяваме това, ние си даваме ясно сметка каква буря от недоволство може да се надигне срещу подобно твърдение в някои среди, които приемат идеята за "квантово изчисление" твърде насериозно, но ние нямаме вина за това.
Като хвърляме "кофа с вода върху нечий пламък", ние не целим нищо друго, освен изясняването на една научна истина, каквато и да бъде тя. Все пак, надяваме се, за всички е понятно, че физичните закони не са нещо, което се "нагажда" или "съобразява" с човешките емоции и пристрастия. И всеки уважаващ себе си учен би трябвало да е готов да посрещне всяко предизвикателство на реалността, колкото и далеч от неговото собствено увлечение да се окаже то...
Квантовата физика като цяло също отиде твърде далеч в стремежа си да се докаже като "последна надежда" на физическите амбиции за "свръхестествени ефекти, неподдаващи се на научно обяснение съобразно здравия разум".
Защото ако няма "квантово изчисление", то няма и "квантова механика" — колкото и трудeн да е за преглъщане подобен "залък" за мнозина — вж. параграф 9.
Ние ще приключим нашето изложение с едно много просто, но (както ни се струва) твърде впечатляващо обяснение на класическите парадокси на Зенон (параграф 10). Според нас, това обяснение е един извънредно "подсказващ" аргумент в подкрепа на основната идея, че ние в действителност живеем в една Вселена, която е в основата си напълно дискретна и детерминистична по природа.
"Всички творения на човешкия ум:
(1) са крайни по отношение на точност на получения резултат и обем на решението;
(2) са локални и детерминистични като прилагани операции в хода на решението"
(Джоул Добржелевски)
Което и да е научно знание (или "теория") може да бъде представено под формата на научна "статия", която съдържа краен брой символи, използвайки някаква крайна азбука. Без значение на използваната азбука и цялостния абстрактен смисъл на статията, ако последната съдържа математически твърдения ("формули") и някакъв краен математически апарат зад тях, тогава тази статия (и научната теория, която тя предлага) е напълно "дискретизируема", и следователно, представима върху универсална машина на Тюринг.
Липсата на непрекъснатост, вероятност, т.нар. "актуална безкрайност", или съмнителни провокиращи ума понятия като "дуализъм" или даже "мултизъм" (мислете си напр. за т.нар. "корпускулярно-вълнови дуализъм", прословутата "котка на Шрьодингер", която може да бъде едновременно жива и мъртва [Sch35], "интерпретация за множественост на световете", предложена от Еверет, и други концептуални заврънкулки, широко използвани в съвременната квантова механика) нямат нищо общо с каквито и да било физични експерименти, които биха могли да ги "потвърдят" или "опровергаят".
И това е едно от най-големите недоразумения, които съществуват в съвременната наука.
"Липсата" на непрекъснатост, вероятност, актуална безкрайност, или дуализми и мултизми от какъвто и да е вид в нашия реален свят, обаче, има нещо общо с тезиса на Чърч-Тюринг; всъщност, тя е директно следствие от последния.
За да бъдем по-точни: това, което ние имаме предвид под "липса" не е, че ние действително смятаме, че тези понятия са "фалсифицируеми" или "отсъстващи" в реалността, а просто илюстрира факта, че ние познаваме по-прост модел (а именно: универсалната машина на Тюринг), който е способен да представи (и пресметне) всички математически следстствия от всички тези понятия без изключение.
Например, всяко понятие за някаква "непрекъснатост" в математиката е представимо под формата на "променлива" (т.е. някакъв символ от някаква крайна азбука); същото е в сила и за понятиeтo "вероятност".
Без значение на това колко сложни могат да ни изглеждат тези понятия (и съответните теории, които си служат с тях) в нашето въображение, крайната (и проста) истина е, че ние дори не можем да си представим как едно понятие или теория би изглеждало, ако то не е (?) преставимо върху универсална машина на Тюринг.
Решителният аргумент в полза на дискретността и детерминизма, предложени от тезиса на Цузе-Фредкин, е един принцип, известен в метафизиката като "Бръснач на Окам".
Дефиниция ("Бръснач на Окам"): Ако имаме две (или повече) съперничащи си физични теории, които обясняват едно и също физично явление, то тогава ние избираме да използваме най-простата възможна теория/обяснение.
Бръсначът на Окам, макар и често цитиран от физиците, е вероятно една от най-подценяваните концепции в съвременната физика.
В този смисъл, онова, което ние имаме предвид по-горе под "липса", е всъщност още един начин да заявим, че ние разполагаме с друго, по-минималистично (т.е. "по-просто") представяне на тези понятия, което ни позволява да гледаме на Вселената така, сякаш Тя е фундаментално дискретна и детерминистична по природа.
Или, другояче казано:
Универсалната машина на Тюринг (или който и да е универсален компютър) ни помага да намерим "съответствия" на всички други "неясни" понятия върху множество от крайни, добре дефинируеми понятия като "бит" и "програмна инструкция" (т.е. крайно множество от "команди", или "правила" — ако говорим за клетъчни автомати — по същество, един информатичен еквивалент на математическото понятие за функция върху крайно множество от дискретни елементи).
За по-добро разбиране на тази тематика, бихме могли да си послужим със следната таблица:
| "Непрекъсната" математика и физика | Дискретна математика и цифрова физика |
| актуална безкрайност | потенциална безкрайност (под формата на безконечно разширяема "външна памет", т.е. "лента", ако говорим за машина на Тюринг например) |
| непрекъснатост | краен алгоритъм (т.е. "компютърна програма"), която е способна да се изпълнява неограничено дълго време, изчислявайки напр. някое "реално число" с каква да е отнапред зададена точност |
| "действителна" вероятност и случайност | псевдо-вероятност и псевдо-случайност (генерируема алгоритмично от генератор на псевдо-случайни числа) |
| дуализъм/мултизъм | алгоритмични процеси ("нишки"), които се изпълняват при пълен паралелизъм |
Нека сега да забележим, че понятия като "дискретност" (т.е. всичко "недвижимо" под формата на комбинация от битове) и "детерминизъм" (т.е. всичко "в движение" под формата на операции върху множество от елементарни "недвижими обекти", или битове) не могат да бъдат редуцирани по-нататък:
Наистина, няма начин да се минимизират "по-нататък" понятия като "бит" или "инструкция", особено ако тази "инструкция" е единствена, точно както в случая с единственото правило при клетъчните автомати!
Тезисът на Чърч-Тюринг прави "аморфни", "неизкристализирали" понятия от "непрекъснатата" математика и физика най-накрая да придобият форма в кристално ясни концепции от дискретната математика и информатика, а именно: дискретност, детерминизъм и крайност (за да бъдем точни: "разширяема крайност", т.е. "потенциална безкрайност").
Например, различни видове вероятности и недетерминистични3 машини на Тюринг биха могли да бъдат построени, но за всички тях може да бъде доказано, че те имат изчислителна мощност която е равна (или не превишава) изчислителната мощност на класическата детерминистична машина на Тюринг; математическото доказателство на този добре известен факт може да бъде намерено в кой да е учебник по теоретична информатика.
Подобно, изчислителната яснота на математическия модел, основан на клетъчни автомати, несъмнено надраства и изживява недомислиците на т.нар. "Копенхагенова интерпретация" във физиката, както и нейните модерни наследници, като напр. "интерпретацията за множественост на световете" (MWI)4. Още повече, че за коя да е MWI-теория може да бъде доказано, че тя е еквивалентна на някакъв "многонишков" ("multi-path") изчислителен модел, а последния може да бъде напълно реализиран върху някакъв универсален клетъчен автомат или универсална машина на Тюринг.
Джон Конуей, изобретателят на знаменитата игра "Живот", постави неотдавна интересния въпрос защо (ако Вселената е наистина клетъчен автомат) ние не сме способни да "усещаме" нейната гранулярност/дискретност [CFM02].
Отговорът на този въпрос, както и на всички въпроси свързани с предполагемата "непрекъснатостта на времето и пространството" — така, както се смята в съвременната физика — е твърде прост и той попада в първата категория (A).
Наистина, ако тезисът на Чърч-Тюринг е верен, то тогава всички математически функции/теории, включително коя да е възможна "Теория за всичко съществуващо" (Theory of Everything - TOE), която е била някога предложена (или въобще някога ще бъде предложена), могат да бъдат представени (и изчислявани) върху универсална машина на Тюринг.
Погледнато от някаква определена гледна точка, горното е един наистина забележителен факт: излиза, че всяка TOE (или предложение за TOE) — взета от съвременната физика с нейния привидно непрекъснат математически апарат — може да бъде "трансформирана" (или: "изобразена", "кодирана") върху едно очевидно едномерно дискретно пространство на някаква "лента", и при това пресметната, като се използва четяща/записваща "глава", която оперира на дискретни времеви интервали, движейки се наляво или надясно по лентата, стъпка по стъпка, върху някаква универсална машина на Тюринг.
С други думи, оказва се, че целия диспут относно "истинската природа" на пространството и времето (т.е. дали пространство-времето във Вселената е фундаментално непрекъснато или дискретно) е до голяма степен "релативистичен": може да изглежда донякъде изненадващо, но излиза, че всичко зависи от гледната точка!
Нека да зебележим сега, че нашето физично "усещане", че Вселената е непрекъсната по природа, не е нищо друго освен следствие от образователната система и придобитите с нея навици за мислене: на нас просто ни е била преподавана "непрекъсната" математика и физика в училище и университета, и именно затова ние сме започнали да вярваме в "пространствено-времевия континуум"!5
От друга страна, има сериозна причина поради която всички физични теории, предполагащи дискретност и детерминизъм на Вселената следва да бъдат предпочетени пред всички останали теории, внушаващи противното — а именно, принципът на Окам:
Ако вие разполагате с някаква физична теория, при която пространството е нещо по-просто (?) от дискретна решетка, времето може да бъде предствено като нещо по-просто (?) от дискретни времеви интервали, а физичните закони във вашата теория са нещо по-просто (?) от елеметарни детерминистични функции, то тогава, моля ви, на всяка цена, кажете ни как вашата теория изглежда?!
Очевидно, процесът на "упростяване" не може да бъде развиван "по-нататък".
Все пак, за да можем да разберем защо пространството не е едномерна, а тримерна решетка, ще се наложи да изполваме аргументи от вида (B). А именно, ще трябва да приемем допускането, че Вселената е тримерен клетъчен автомат, а не едномерна машина на Тюринг, така както тезисът на Чърч-Тюринг привидно ни внушава (вж. параграф 7).
Всъщност, основната идея зад тезиса на Чърч-Тюринг не е била базирана изрично върху идеята за едномерно пространство ("лента") и "единствен наблюдател" ("глава"), населяващ това пространство — цялостната идея на тезиса следва да бъде изучавана в много по-широк контекст (параграф 8).
Идеята е била да се покаже конкретен пример на механично конструируема машина, която е способна да "обхване" интуитивната концепция за "универсалност" на изчислението. В този смисъл, няма нищо специално в една универсална машина на Тюринг: последната е просто една от многото възможни реализации на механична машина, за която може да се докаже, че е изчислително универсална.
Обаче универсалната машина на Тюринг определено не е най-добрият пример за универсална изчислителна машина.
Прилагайки принципа на Окам е лесно да заключим, че всяка възможна теория, която приема пространство-времето за хомегенно, би следвало да бъде предпочетена пред коя да е друга теория, която допуска съществуването на някакви "специални" точки в пространство и/или времето, в които физичните закони са различни. В този смисъл, ако ние искаме да конструираме не само универсен, но също и минималистичен (максимално упростен) изчислителен модел, ние трябва да използваме някакви идентични елементи за съхранение на информация ("клетки"), които съхраняват краен набор от елементи ("състояния") и тези клетки променят своите състояния паралелно, използвайки винаги и навсякъде една и съща локална трансформация ("правило").
Но това именно е дефиницията за клетъчен автомат!
Така че, няма никаква изненада в това, че ако ние вярваме в тезиса на Чърч-Тюринг, то ние сме склонни също да вярваме на тезиса на Цузе-Фредкин: клетъчните автомати се явяват нашия най-добър избор, ако ние искаме да използваме изчислителен модел, който е способен да "обхване" всички възможни "интуитивно изчислими математически функции" и ние искаме също нашия модел да се подчинява на принципа на Окам. Така да се каже, клетъчните автомати, които първоначално може да изглеждат като голяма изненада като предлагана основа за математически модел на Вселената, са всъщност не само извънредно "естествени" модели, но също и единствено възможните модели, ако ние искаме да построим теория, която взема предвид както универсалността, така и минималността на модела (т.е. включва в себе си едновременно принципите за изчислителна универсалност и принципа на Окам).
В края на настоящата статия ние няма да пропуснем възможността да отговорим на Джон Конуей, като предложим един прост илюстративен аргумент, основан на играта "Живот" и свързан с древния парадокс за "Ахил и костенурката" (вж. параграф 10).
Ние вероятно бихме могли да направим нашето заключение веднага още тук, ако не беше един "детайл", който днес толкова много тревожи най-добрите умове на теоретичната компютърна наука и теоретичната физика...
"...там няма проблем, има само решения..."
(Джон Ленън, от неговата песен "Гледайки колелата")
Предложеното от Алън Тюринг представяне на класа на всички "ментални функции" върху механична машина (каквато е универсалната машина на Тюринг) все още оставя някакво пространство за спекулации относно някакви възможни квантово-механични, "не-механични", или "супер-механични" методи за изчисление, ако така ви харесва. Но това е само една от възможните интерпретации на тезиса на Чърч-Тюринг.
Онова, което Тюринг всъщност е имал предвид (и той подчертава това, по един или друг начин, на много места в своята статия [Tur36]) е фактически един недвусмислен начин за извършване на изчисление, т.е. чисто "ментален" начин да се опише изчислението като процедура от типа "разум, молив и хартия". В този смисъл, "разум" следва да бъде разбиран като еквивалент на "вътрешно състояние" ("състояние на регистъра") на някаква универсална машина на Тюринг (УМТ), "молив" е еквивалент на "глава", която чете и записва символи и се придвижва с по една стъпка наляво или надясно и, разбира се, "хартия" е еквивалент на "лента", която съхранява външната информация за тази УМТ.
Сега, ако някой направи някакво определено усилие да престане да си мисли за една УМТ като за "механична машина" (т.е. устройство, което може да бъде конструирано само от механични части), и се постарае наместо това да погледне на нещата от друг възможен ъгъл, а именно, че тази УТМ е просто един точен и недвусмислен начин да си мислим за научния процес като за процедура "разум, молив и хартия", то този някой сигурно може да достигне до една определена гледна точка, в която да направи следното удивително откритие:
Наистина, няма никакво значение какво можем да наблюдаваме във външния (заобикалящия) ни свят или посредством физични експерименти в някаква лаборатория; единственото, което наистина има някакво значение, е какво може да бъде достигнато, ако човек използва само и единствено своя собствен разум!
Или, казано още по-точно с други думи:
Ако нещо не може да бъде получено, използвайки само "мисловни експерименти", то това нещо не може да бъде получено използвайки какъвто и да е друг вид физични експерименти.
Тази гледна точка е наистина много интересна, и именно такава всъщност е и основната идея на Цифровата Физика (ЦФ) — нова научна област, предложена от автора на настоящата статия. Въпреки името си, цифровата физика не е просто "още една теория за физиката — такава, каквато я познаваме", а е по-скоро теория за това как физиката би следвало да изглежда, ако ние приемем тезиса на Цузе-Фредкин за верен и се опитаме да се концентрираме върху основния въпрос:
"Ако Вселената наистина е клетъчен автомат (КА), то какъв именно КА тя би следвало да бъде?"
Основната идея тук се състои не в това да изучаваме "външния свят" и да се опитваме да "вградим" колкото се може повече познати ни от физиката характеристики в този КА модел6, а просто да се опитаме да "компресираме" (или "представим") всички възможни "вътрешни" мисловни модели, т.е. алгоритми, върху някаква конкретна пространствена топология ("дискретна решетка"), като използваме някакво конкретно фиксирано правило за клетъчен автомат, започвайки от някаква фиксирана крайна начална конфигурация, която поражда всички тези алгоритми без изключение [Pet02b].
Подобно на тезиса на Чърч-Тюринг, за който можем да кажем, че е някакъв вид "компресия" на всички известни ни абстрактни понятия, като "непрекъснатост", "случайност", или "актуална безкрайност" върху едно по-тясно множество от понятия като "дискретност", "псевдослучайност (т.е "алгоритмична случайност", или "детерминизъм"), и съответно, "потенциална безкрайност" (вж. таблицата по-горе), цифровата физика — такава, каквато ние я виждаме — е също някакакъв вид компресия, но този път на ниво клетъчни автомати.
Както ние ще демонстрираме в следващите статии от тази серия [Pet02], този почти фантастичен подход не е просто плод на въображението. Това е подход, който наистина работи и произвежда резултати в термините на математически ограничения, които следва да бъдат верни за "Автомата", за който се предполага, че е изоморфен на нашата Вселена.
---
В нашата работа [Pet02f] ние описваме схема, която превръща всеки абстрактен математически модел за клетъчен автомат в паралелна машина, която може да бъде конструирана по принцип в реалния свят.
Макар тази механична машина (за разлика от абстрактната дефиниция за клетъчен автомат) да не променя състоянието на всички свои клетки "мигновено", а по-скоро асинхронно, тя работи по такъв начин, че за всеки локален наблюдател, който живее "вътре" в такава машина всичко изглежда така, сякаш той (или тя) живее в една Вселена-Клетъчен Автомат, който работи при пълен паралелизъм.
Също както и класическата УМТ, описана от Тюринг в [Tur36], нашата паралелна машина е напълно механично устройство, което не използва каквито и да било квантово-механични ефекти.
Също, в [Pet02m] ние демонстрираме едномерен клетъчен автомат, който произвежда истински квантово-механични (а именно, EPR) ефекти, без да използваме каквато и да било "квантово-механична магия".
Ето защо, ние сме склонни да вярваме, че сега модерното "квантово изчисление" (КИ) може да се окаже една от най-забележителните научни заблуди на всички времена: няма "ускорение" на изчислението, използвайки "квантово-механични" ефекти, просто защото същите ефекти могат да бъдат получени върху класическо, т.е. напълно механично устройство, каквото именно се явява всеки клетъчен автомат.
---
Единственото сериозно възражение срещу тезиса на Чърч-Тюринг (и, като следствие, срещу тезиса на Цузе-Фредкин) дойде от поддръжниците на идеята за т.нар. "квантово изчисление" (КИ).
Това именно възражение ние наричаме "контрааргумент за скоростта на изчисление", и то може да бъде формулирано както следва:
"Ако квантовите компютри и да не са способни да решават други задачи, които класическите (механични) компютри не могат да решават, то те (квантовите компютри) все пак биха могли да решават някои определени задачи по-бързо от обикновените такива."
Всички други аргументи (относно привидно "непрекъснатата" природа на пространство-времето, различни аргументи, свързани с принципа на Хайзенберг за "фундаменталаната вероятностна природа" на физиката, и др. под.) не биха могли да се смятат за сериозна "заплаха" за верността на тезиса на Цузе-Фредкин, а по-скоро обикновено показват едно фундаментално неразбиране, разпространено най-вече във физичните среди, за това какво изобщо е тезиса на Чърч-Тюринг и теоретичната информатика като цяло.
Но споменатото по-горе възражение е един наистина сериозен контрааргумент, който действително заслужава нашето внимание.
Всъщност (както ние ще видим по-долу), тезисът на Чърч-Тюринг наистина е една незряла форма на тезиса на Цузе-Фредкин, просто защото двумерните и тримерни клетъчни автомати могат да решават някои изчислителни задачи по-бързо от класическата УМТ (която, на свой ред, за по-голяма яснота, може да бъде разглеждана и като едномерен КА).
В този смисъл, не само понятието за "изчисление", но също и представата за "универсалност" би следвало да бъдат предефинирани така, че да включват не само понятието за "изчислимост" (по принцип) на някаква математическа функция, но така също и времето, използвано за пресмятане на тази функция.
Поддръжниците на "квантовото изчисление" може да се окажат твърде оптимистични в своите твърдения, но те са забелязали един твърде интересен пропуск в дефиницията на тезиса на Чърч-Тюринг, който със сигурност не е бил дискутиран в средата на тридесетте години, когато това понятие възниква. И, твърде вероятно, изобщо никога не е бил дискутиран.
Цялата представа за "скорост на изчислението" на някаква математическа функция има твърде малко смисъл в класическото разбиране за "математика": елементът "скорост" е бил разпознат като важен едва с появата на модерните компютри през шестдесетте, и като следствие — на теорията за изчислителната сложност.
И дори с появата на модерните елекронни компютри проблемът за "скоростта на изчисление" — във връзка с дефиницията на тезиса на Чърз-Тюринг — все още остава в сянка поради следните две основни причини:
Както Дейвид Пиърсън описва това в [Pea96]:
"[...] дори ако ние днес бихме разполагали с компютър, базиран на кристална решетка, ние просто не бихме знаели как да го използваме. Програмирането е дотолкова добре разработено под схемата на фон Ноймановия модел, че е действително невъзможно да го премахнем от нашето мислене. Очевидно, ние просто можем да програмираме някакъв клетъчен автомат да емулира някаква стандартна фон Нойманова машина [...] — това определено може да бъде направено [...]. Но такъв подход не използва преимуществото на допълнителната изчислителна мощност, която клетъчните автомати имат. За да я използваме ефективно, ние трябва да бъдем подготвени да променим нашия програмен модел.
Онова, което клетъчните автомати ни предлагат, е паралелизъм, способност да се извършва много голям обем изчисление по едно и също време. Паралелните машини обещават да бъдат на "предния фронт" на високо-скоростното изчисление, и действително, всеки голям играч в областта на суперкомпютрите предлага някаква масивно-паралелна машина. За нещастие, това обещание беше правено най-малко в продължение на последните 30 години, от ерата на ILLIAC IV насам, и никога не е било изпълнено. Има значителни проблеми, които трябва да бъдат преодолявани при разработката на паралелни компютри — синхронизация, програмни конструкции, локалност на данните, взаимосвързаност на мрежите, разпределена памет, и модели за множеството от програмни инструкции — са само някои от тях. Конвенционалните компютри винаги успяваха да догонят паралелните такива по отношение на скоростта на изчисление преди тези проблеми да бъдат превъзмогнати."
И също:
"Трудностите при писането на софтуер за паралелни машини са добре известни. [...] За нещастие, автоматичните техники като цяло дават като резултат, да речем, 5-кратно разпалеляване на някакъв изчислителен процес, а този малка константа на увеличение не е достатъчна да издържа усилията в разработката на проекта — последователните машини ги настигат много бързо, в частност защото паралелните машини изискват по-дълъг период за разработка. [...] Поради тези страхотни трудности, поради това, че паралелните машини се провалиха да докажат своите обещания за последните 30 години, и след няколко банкрупта и провалени проекта, някои наблюдатели обявиха паралелизма за мъртъв. Като гледаме достатъчно далеч напред, възкресяването е очевидно на път, но предизвикателствата си остават, и ние трябва да се преборим с тях преди компютрите, основани на кристална решетка, да станат реалност."
---
На това място, някой внимателен читател може да се окаже достатъчно прозорлив да зададе следния интересен въпрос:
"Е добре, ние казваме, че една УМТ може да пресмята всичко мислимо от човешкия ум. В настоящата работа ние казваме още, че не е важно да се наблюдава "външния" свят или да се правят експерименти в някаква лаборатория; единственото важно нещо е да седнем на един стол, да вземем молив и лист хартия, и да се концентрираме върху мисловни експерименти, като използваме единствената "лаборатория", с която всеки от нас разполага — нашaта собствена глава.
Добре, това изглежда доста интересно и провокиращо ума... Но все пак, защо ние казваме, че тезиса на Чърч-Тюринг е в действителност една неразвита форма на тезиса на Цузе-Фредкин? Къде именно лежи границата между двете твърдения?
Защото, ако ние допуснем, че няма никаква разделителна линия, то ние можем лесно да стигнем до извода, че нашата Вселена не е тримерен клетъчен автомат, а просто някаква жалка едномерна лента, която освен това "оперира" последователно, както това прави една универсална машина на Тюринг?
В края на краищата, защо, за Бога, ние трябва да изоставим добре познатата ни, приета за "стандарт" идея за изчисление върху универсална машина на Тюринг и да я заменим с новата идея за изчисление върху универсален клетъчен автомат? Защо Вселената не е последователна едномерна УМТ, а е тримерен паралелен компютър, изоморфен на клетъчен автомат?"
Това е един доста добър въпрос, наистина! (И ако читателят е бил способен да достигне сам до подобен въпрос, то тогава той определено заслужава нашите поздравления...)
Този въпрос има отговор, но за съжаление този отговор е достатъчно дълъг, за да заслужава цяла една отделна статия [Pet02g].
Със заглавие на статия като тази ("Какво е емулация?") сигурно трудно може да се предположи, че там има наистина нещо ново, което може да бъде казано. В края на краищата, не е ли "емулацията" един доста ясен и добре установен термин в компютърната наука?
Но, както се оказва, тя не е!
Изненадващо, оказва се, че двумерните и тримерни клетъчни автомати могат да решават някои определени изчислителни задачи по-бързо от едномерните клетъчни автомати, и този прост факт има невероятно големи следствия които, твърде вероятно, никога до сега не са били забелязвани и анализирани подобаващо от теоретичната компютърна наука.
Защото, ако тезисът на Чърч-Тюринг наистина беше някаква крайна форма, "обхващаща" всички изтънчени детайли в дефиницията на понятието за "интуитивно изчислима математическа функция/теория", то тогава наистина би следвало, че нашата Вселена е действително един едномерен автомат (т.е., някаква УМТ)!7 Но, очевидно, случаят не е такъв: ние живеем в една Вселена, в която просто накак-си се е "случило" да има три измерения, поне пространствено.
Следователно, нещо липсва!
Очевидно, тезисът на Чърч-Тюринг е бил неспособен да "обхване" някакъв изтънчен детайл от понятието за "изчисление", и този детайл е останал неразкрит до сега.
Този именно детайл е проблемът за "скоростта на изчислението".
След всичко казано дотук сега вече ние сме достатъчно подготвени да формулираме едно важно твърдение, което ние ще предстваим по-долу в следните три по същество напълно еквивалентни форми:
Тезис на Фредкин-Петров (или: "Тезис за тримерния универсален КА"): Вселената е тримерен универсален клетъчен автомат.
Тезис на Фредкин-Петров в математическа форма (или: "Тезис за тримерния универсален КА в математическа форма"): Класът на всички интуитивно изчислими математически функции съвпада с класа на функциите, изчислими върху тримерен универсален клетъчен автомат.
Тезис на Фредкин-Петров в информатична форма (или: "Тезис за тримерния универсален КА в информатична форма"): Класът на всички интуитивно дефинируеми алгоритми съвпада с класа на всички алгоритми, изчислими върху върху тримерен универсален клетъчен автомат.
Няколко важни бележки:
Един интересен начин да погледнем върху нещата е да си мислим за подхода на Тюринг (основан на идеята за единствена "глава", или самотен "наблюдател", който "пътува" в едно едномерно пространство, променяйки своето "вътрешно състояние", или "ум") като за някакъв "егоистичен" подход. В сравнение с него, на "клетъчно-автоматния" подход (основан на идеята за "съвкупност от можество клетки", или "умове", които "работят" в обстановка на пълен паралелизъм, изчислявайки съвместно някакъв неизвестен никому поотделно алгоритъм) можем да гледаме като на подход, съответстващ на нещо като "съобщество от разумни единици".
Тази гледна точка, по-подходяща за научни области като "Изкуствен Интелект" (Artificial Intelligence) или "Изкуствен Живот" (Artificial Life) отива малко встрани от "обсега" на темите, засягани в настоящата статия и Цифровата Физика като цяло. Но ако тя би била от някаква полза за читателя, то такъв поглед върху нещата също би могъл да бъде разглеждан.
Може да си мислим, че тезисът на Цузе-Фредкин всъщност заменя тезиса на Чърч-Тюринг, предполагайки неща за нашия реален свят, които са "по-естествени" и "пасват по-добре" към настоящата сфера на изследвания в области като Изкуствен Интелект и Изкуствен Живот, напр.:
"Вселената не съдържа единствено разумно същество/наблюдател, който има участта да извършва някакво изчисление в някакво "мъртво" пространство, което твърде много наподобява някаква едномерна "лента" или "хартия", а е всъщност съставена от множество малки живи елементи (множество "разумни единици", или "наблюдатели"), всеки от които комуникира с останалите, разменяйки "идеи" или "информация"."
"Квантовата механика е цялата там!"
(Ричард Фейнман към Едуард Фредкин, насърчавайки го да продължи работата си в областта на клетъчните автомати [Fre01])
Може да се запитаме:
"Колко дълго би следвало да чакаме най-добрите умове в съвременната теоретична физика най-сетне да се "успокоят" и "разпознаят" очевидната елегантност и мощ на тезиса на Цузе-Фредкин? Или, може би, също както при случая с Чърч-Тюринг-Пост-Марков и др. (вж. нашите исторически бележки по-горе), ние ще имаме съдбата да чакаме със затаен дъх някой нов "квантово-механичен фокус-бокус" да изникне в поредната статия, публикувана в някое "уважавано физично списание", за да може по-късно да го опровергаем, показвайки неговата еквивалентност с някой добре известен напълно механичен изчислителен модел?!8"
Добрата новина е:
"Не, няма да има нужда да минаваме през този "порочен кръг" до безкрай: ако Вселената наистина е механично изчислително устройство, и ние сме спосособни да построим някаква "Теория за всичко съществуващо" (ТОЕ), базирана на тази идея, то тогава всички останали потенциални "заплахи" за тази идея ще бъдат лесно проверявани и отхвърляни".
Лошата новина е, обаче:
"Докато ние не разполагаме с ТОЕ, базирана на тезиса на Цузе-Фредкин, т.е. докато не знаем кой е конкретният клетъчен автомат, за който може да се смята, че е изоморфен на нашата Вселена, гледната точка, че "квантовата механика е просто механика" е все още уязвима".
Както Йоги Бера го е казал: "Играта не е свършила дотогава, докато не е свършила".
Все пак, нашето очакване е, че идеите зад тезиса на Цузе-Фредкин ще бъдат лесно приети, когато "точният" клетъчен автомат бъде намерен; може даже да се обзаложим, че след като това бъде направено, само за година или две, идеята ще бъде възприета във всички по-значими научни кръгове, подобно на тезиса на Чърч-Тюринг, който е бил предложен и приет някъде през 1936-37 г.
Голямата трудност по посока на някакво значително научно приемане на идеята на тезиса на Цузе-Фредкин лежи в неговата чисто абстрактна форма. За разлика от универсалните машини на Тюринг, които лесно могат да бъдат конструирани и за тях да бъде демонстрирано, че са "универсални" (по всички възможни начини и съгласно всякакъв "здрав разум", който всеки индивидуален изследовател може да влага в понятието за "изчислителна универсалност"), тезисът на Цузе-Фредкин не ни дава някакъв конкретен пример за подобен клетъчен автомат, а просто "предсказва" неговото съществуване.
Но всичко това е доста разбираемо, наистина: може да дадем веднага много примери за универсални машини на Тюринг, но пример за универсален клетъчен автомат, който при това съвпада с TOE, определено може да има само един!9
---
Ако ние се съгласим, че от тезисът на Чърч-Тюринг следва, че всички математически функции са механично изчислими 10, то тогава тезисът на Цузе-Фредкин е податлив на възражения от привържениците на "квантовото изчисление" единствено по отношение на проблема със "скоростта на изчисление".
За да подчетаем колко важна е тази точка от нашето изложение, ние бихме искали да повторим горното твърдение в малко по-разширена форма:
Ако поддръжниците на идеята за "квантово изчисление" искат да могат да продъжат да защитават по някакъв начин своя контрааргумент (спорния въпрос дали квантовите компютри ще могат да демонстрират "скорост на изчисление" по голяма от конвенционалните), то тогава единствения път (буквално!), по който те биха могли да поемат, е да се опитат да предложат някакви други, подобни на EPR корелации, да ги наблюдават експериментално, и после да докажат някакви теореми, подобни на тази на Бел, но този път като отчитат факта, че физичните закони на Вселената могат да се окажат напълно детерминистични.
Но ние се съмняваме, че нещо подобно ще бъде открито когато и да било.
Всичко останало следва да бъде оставено да почива в мир, и на него може да се гледа просто като на "исторически бележки" върху развитието на идеята за тъй дългоочакваната "Теория за всичко съществуващо"...
---
Тази статия е написана от перспективата на теоретичната информатика.
Нейната основна аудитория от читатели вероятно ще бъдат преди всичко специалистите в областта на теоретичната информатика, изследователите в сродни области като "Изкуствен Интелект" или "Изкуствен Живот", или просто компютърните програмисти, които все още харесват своите "старомодни" (според някои) компютри — "простите играчки" на днешия ден, които (о, чудо!) не съдържат никаква квантово-механична магия, но са все още полезни, някак-си.
Основна цел, която си поставяме с настоящата работа, е да се опитаме да предадем едно просто послание към всички онези, които все още се чудят какво е "квантовото изчисление" и целия голям шум, който се вдига около него напоследък:
"Ами, вярвате или не, целият този шум е за нищо. Буквално!"
Ние съзнаваме, че в момента има твърде много страсти около квантовото изчисление и си даваме сметка, че правейки изказвания като горното неизбежно ще предизвикаме яростния гняв на някои среди в обществото от физици.
Все пак, ние се радваме, че можем да направим подобно изказване. Просто няма от какво да се страхуваме: след години, прекарани в размисли относно "квантовото изчисление", ние най-накрая имаме модел [Pet02m], който демонстрира как EPR работи за клетъчните автомати. И, забележете, нашият модел е конкретен клетъчен автомат, а не някаква проза на тема "как някой би могъл евентуално да конструира подобен автомат".
От наша гледна точка, квантовото изчисление е просто един "хартиен дракон"11, който в настоящия момент се използва (макар и несъзнателно) като своеобразно "плашило", което отвлича теоретиците в областта на информатиката встрани от правилния път.
И, повярвайте ни, правилния път, по който трябва да се поеме оттук нататък, не се нарича "квантово изчисление" или "квантова физика"; той се нарича "цифрова физика", и ние се надяваме, че ще разполагаме с достатъчно време и място да го опишем в детайли в бъдещите статии от тази поредица [Pet02].
За всички останали, които все още вярват, че "има някакъв шанс" за квантовото изчисление най-накрая да изпълни своите "обещания", ние можем да кажем само, че сме уверени, че там изобщо няма никакъв шанс, но както и да е...
Онова, което ние научихме през всичките тези години е, че няма никакъв начин да убедим всички в тези безкрайно прости неща, които ние се опитахме да изложим тук с безкрайно прости аргументи...
Почти единственото, което бихме могли да направим за онези, които "все още не са убедени" в това, за което говорим по-горе, е да седнем ей тук удобно и да си припомним мъдрите думи на една прекрасна песен:
"Хората задават въпроси, поддали се на суетата наоколо.
Добре, аз им казвам, че там няма никакъв проблем, има само решения.
Ами те просто поклащат глави и ме поглеждат така, сякаш съм загубил ума си.
Аз им казвам: няма за къде да бързаме...
Аз просто си седя тук и си прекарвам времето,
Просто си седя тук, гледайки как колелата се въртят и въртят, въртят и въртят..."
(Джон Ленън, "Гледайки колелата")
И така, колко дълго ще трябва да чакаме физичното общество да се съгласи с тези прости неща, които ние се опитваме да изложим чрез настоящата статия?
Ами, ние не знаем... Нас просто не ни е особено грижа за това. (Поне дотолкова, доколкото модното сега "течение" не отвлича твърде много "умове" от областта на теоретичната информатика....)
Ние се намираме в просто състояние на ума и духа; ние сме в една ситуация, където няма нужда от излишно бързане. Просто можем да си седим тук, прекарвайки си времето, очаквайки търпеливо, но уверено, че промяната ще дойде, просто гледайки как "колелата се въртят, въртят и въртят"...
"Зенон излага 40 различни парадокса, които се явяват следствие от предположението за множествеността и движението, всичките те явно базирани на трудностите, произхождащи от анализа на континуума."
(Прокъл)
"В този капризен свят нищо не е по-капризно от посмъртната слава. Една от най-забележителните жертви на неспособността на потомството за справедливо отсъждане е Зенон от Елеа. Макар да е измислил четири аргумента, всичките те несъизмеримо изтънчени и дълбоки, огромното мнозинство от по-сетнешни философи го определят просто като остроумен жонгльор, и всичките негови аргументи като софизми. След две хиляди години на непрекъснато отричане, тези софизми бяха изложени наново, и станаха основа на математически ренесанс..."
(Бертранд Ръдел)
"Макар те често да са били отхвърляни като логически глупости, много опити са били също направени да се отървем от тях с помощта на математически теореми, като тези от теория на сливащите се редици или теория на множествата. В края на краищата, обаче, трудностите присъщи на неговите аргументи винаги се връщаха обратно със същата сила, защото човешкият ум е така устроен, че той може да гледа на континуума по два възможни начина, които не се погаждат твърде много един с друг."
(Енциклопедия "Британика" за парадоксите на Зенон)
Почти всичко, което знаем за Зенон от Елеа (ок. 490 г. пр.Хр. – 425 г. пр.Хр.) може да бъде намерено на първите страници от съчинението на Платон "Парменид"12.
Според Платон и Прокъл, през своите младежки години Зенон разработва 40 различни парадокса13, написани в книга. За съжаление — поне както твърди легендата — тази книга е била открадната, така че повечето от тези парадокси не са запазени.
Парадоксите, които Зенон дава за движението на телата, са вероятно най-известните и най-объркващите. Аристотел, в своята работа "Физика", дава четири от аргументите на Зенон, известни като парадокси за "Дихотомията", "Ахилес и костенурката", "Стрелата" и "Стадиона".
По-долу ние ще разгледаме само първите два от тях.
Относно "дихотомията", Аристотел описва аргумета на Зенон както следва [Hea21]:
"Няма движение, защото това, което се движи, трябва да достигне средата на пътя, преди да пристигне в неговия край."
За да се измине някаква отсечка, необходимо е да се достигне нейната среда. След това трябва да се достигне 1/4 част от остатъка от пътя, след това трябва да се достигне 1/8 част, и т.н. до безкрайност. Оттук следва, че движението никога не завършва.
Аргументът тук не се отхвърля с посочване на факта, че добре известната безкрайна сума дава единица:
1/2 + 1/4 + 1/8 + ... = 1.
Вероятно Зенон би могъл да отговори на това с контрааргумент, че сумата 1/2 + 1/4 + 1/8 + ... всъщност никога не достига 1, но още по-объркващ за човешкия ум е опита да се сумира 1/2 + 1/4 + 1/8 + ... в обратен ред. Преди да изминем единица дистанция, ние трябва да достигнем средата на пътя, а преди да се окажем там, ние трябва да сме изминали 1/4 от пътя, но преди да изминем 1/4 от пътя, ние трябва да сме изминали 1/8 от пътя, и т.н.. Този аргумент ни кара да осъзнаем, че всъщност ние никога не бихме могли да започнем(!) движението, тъй като се опитваме да построим тази безкрайна сума от "погрешния" край. Наистина, това е един изкусен аргумент, който все още озадачава човешкия ум дори днес.
С други думи, парадоксът се е заключавал в следното:
"... пропътуването на безкрайно число от крайни дистанции, които, както Зенон би искал ние да заключим, трябва да отнеме безкрано време, всъщност никога няма да завърши. И тъй като аргументът не зависи от дистанцията или от това кой или какво пътува, оттук следва, че няма такава крайна дистанция, която изобщо някога може да бъде пропътувана, а оттук пък следва, че движението изобщо е невъзможно." [Hug02]
Обаче, този парадокс е лесно разрешим, ако ние погледнем на света през призмата на клетъчните автомати:
"Един електрон, във Вселената на Фредкин, не е нищо друго освен "конфигурация" от информация, и един електрон, който обикаля по някаква орбита, не е нищо друго, освен тази конфигурация в движение. Разбира се, дори това движение е в някакъв смисъл илюзорно: битовете от информация, които съставят тази конфигурация, никога не се движат [...]. Всеки бит си стои "на място" и ограничава своята активност единствено до "премигване" между "включено" и "изключено" състояние." [Wri88a]
Нека да забележим сега, че клетъчните автомати с присъщото им свойство да съдържат "конфигурации", които се "движат", без в действителност да има движение (да си мислим напр. за един глейдер в играта "Живот"), и тяхната пространствено-времева конструкция, която е напълно дискретна, изглеждат като перфектно предложение за абстрактен математически модел, който обяснява едновременно и двата спорни въпроса, свързани с парадокса:
Най-знаменития от аргументите на Зенон срещу непрекъснатостта на пространство-времето е без съмнение този за Ахил. Според Аристотеловата "Физика", парадоксът се заключава в следното:
"... по-бавния, който бяга, никога няма да бъде задминат от по-бързия; защото това, което преследва, първо трябва да достигне точката, от която това, което бяга, е започнало, така че по-бавния би трябвало непременно да бъде някаква дистанция по-напред." [Hea21]
Традиционното описание на този парадокс обикновено изобразява древногръцкия герой Ахил, който се надбягва с някаква костенурка, която се движи много по-бавно от него, но той така и не успява да я догони: всеки път когато Ахил достига мястото, където костенурката е била преди малко, последната използва времето, за да се придвижи някаква (незначителна) дистанция напред, и така до безкрай.
И отново, в дискретното пространство-време такъв парадокс не възниква:
Да си мислим за две конфигурации в играта "Живот", да речем два "космически кораба", които пътуват по една и съща линия и в една и съща посока. Нека първият да е "тежък" (т.е. "бавен"), а вторият — "лек" (т.е. "бърз") космически кораб. Ще достигне ли втория космически кораб изобщо някога точка, в която да "догони" първия кораб?!
Безусловно!
(Дори ако приложим процедурата, описана от Зенон – вж. Фиг. 6)
Фигура 6: В играта "Живот" ние наричаме всички движещи се конфигурации, които имат свойството да се преместват в пространството, съхранявайки своята форма, "космически кораби" (на англ.: "spaceships"). "Глейдерът" от Фиг. 3c е пример за "най-лекия" (т.е. най-малкия като брой съставящи клетки) космически кораб.В играта "Живот" е прието скоростта на движение на шахматния цар да се нарича "скорост на светлината" (Конуей избира тази фраза, защото това е най-високата скорост, с която каквото и да е движение може да се случва върху полето). Обикновено скоростта на светлината се означава като c и скоростта на движение на всички космически кораби се измерва относно тази константа. Така например, "глейдерът" се движи диагонално със скорост една четвърт от тази на светлината, т.е. c/4.
Два други космически кораба са показани по-горе. Първия ("по-лекия") от тях е бил открит от Дийн Хикерсън и е бил наречен "костенурка". Тази конфигурация има свойството да се движи ортогонално със скорост c/3.
Другия ("по-тежък") космически кораб е бил намерен от Хартмут Холцуърт, но не му е било дадено някакво специално име. За целите на нашето изложение нека да наречем тази конфигурация "Ахил", тъй като тя до известна степен наподобява мускулесто човешко тяло. Оказва се, че "Ахил" се придвижва ортогонално в пространството със скорост c/2, т.е. той е по-бърз от костенурката.
Нека сега да организираме състезание между Ахил и костенурката в царството на играта "Живот". Първоначално, ние даваме на костенурката 20 клетки предимство. Ще успее ли някога по-бързата конфигурация ("Ахил") да достигне по-бавната ("костенурка")?!
Несъмнено!
(Дискретното пространство-време не е безкрайно делимо, така че дори да решим да приложим процедурата, описана от Зенон, никакви парадокси няма да се появят!)
Нека сега да забележим, че "обясненията", давани на парадоксите на Зенон в традиционната "непрекъсната" математика или физика всъщност нищо не обясняват. Те просто изчисляват "точката на срещата", в която Ахил достига костенурката, но определено не обясняват парадокса, а именно, защо все пак процедурата, предложена от Зенон за пресмятане на пространствено-временната позиция на "рандевуто" води до "безкраен алгоритъм"14.
Много просто казано: те нямат обяснение изобщо.
Подобно, квантовата механика не обяснява EPR или който и да е друг "квантово-механичен" парадокс; тя просто изчислява крайния резултат от даден физичен експеримент, но не дава каквато и да било смислена интерпретация за това какво всъщност става по време на самия експеримент.
Както вече отбелязахме в [Pet02a1], независимо от всички обяснения, които могат да бъдат дадени в защита на тезиса на Цузе-Фредкин, мнозина ще са склонни да отказват да признаят неговата валидност, често без дори да изслушат предлаганите аргументи.
Някои ще са склонни да отричат тезиса просто защото той им изглежда толкова "неестествен", или "странен"; други имат склонността да задават безкрайна поредица от въпроси, която в крайна сметка или разкрива някаква неосведоменост за последното развитие в областта на науката, или даже може да загатва за някакви пропуски в тяхното образование, често включващо сериозно неразбиране за това какво е математиката или теоретичната информатика и за какво става въпрос изобщо.
Парадоксите на Зенон, "котката на Шрьодингер", както и този на Айнщайн-Подолски-Розен, са по същество аргументи срещу "фундаменталната" непрекъснатост на пространство-времето и съществуването на наистина "случайни" събития в нашата Вселена. Докато всички тези аргументи са извънредно изтънчени и дълбоки по своята същност, конвенционалната физика не изглежда да се вслушва в тях достатъчно внимателно.
Квантовата механика просто ги игнорира, или "хитрува", като се опитва да тълкува нещата като аргументи в нейна полза(?):
Зенон е бил разглеждан просто като някакъв "словесен жонгльор"; има някои физици, които съвсем насериозно вярват, че "котката на Шрьодингер" може да съществува в някакво "размазано квантово състояние", в което да е едновеременно жива и мъртва; аргументите на Айнщайн срещу "завършеността" на квантовата механика са били взети като подходяща възможност да се въведат понятия като "фундаментална нелокалност" — по същество, последното не е нищо друго освен въвеждане на концепция за "призрачно действие от разстояние" — в сериозната научна литература.
И, накрая, теоремата на Бел [Bel64] е била "интерпретирана" като "математическо доказателство"(?), че локални модели като клетъчните автомати са неспособни(?) да демонстрират квантово-механични (EPR) ефекти — един "аргумент", за който лесно може да бъде показано, че е просто една глупост [Pet02m].
Макар и да е възможно развенчаването на псевдо-науката да се прави методично, "стъпка по стъпка", все пак е доста тъжно да се види човешкия интелект въвлечен в "произвеждането" на планини от "научни" статии, които нямат никаква научна стойност изобщо. Понижаването на нивото на ненормално разрастналия се егоизъм на техните автори — нещо, което ги прави слепи в преследването на "квантови призраци" и "истински чудеса", наместо да се търсят действително научни обяснения на новооткрите феномени — е нещо, което определено би било от полза.
(Но егоизмът обикновено е смятан за духовна, а не за научна тематика, така че ние ще прекратим с нашите размисли по тази тема дотук...)
И отново, единствената причина, поради която ние сме започнали да вярваме в тази нелепост, е следствие от образователната система:
За дъго време ние не сме разполагали с каквато и да било смислена алтернатива (т.е. някаква друга математическа парадигма, която да е била способна да разреши всички "парадокси", така типични за квантовата механика), и това е причината ние да започнем да вярваме, че именно така стоят нещата в микро-света в действителност!
(И мнозина са започнали да учат другите на тази логически противоречива теория, наместо ясно да идентифицират проблемите и да се опитат да намерят някакво друго решение...)
Защото, в края на краищата, всички парадокси са всъщност ясни математически индикатори, че нещо в някаква теория е фундаментално погрешно (без значение дали говорим за квантовата механика или нещо друго).
Всички парадокси могат да бъдат сведени до логически следствия от вида:
Но, както е добре известно от елементарната логика, от верността на горното може да се изведе логически всяко друго твърдение. Ето защо, подобни парадокси не са просто някакви "малки незначителни парадоксчета, които ние можем да наблюдаваме тук и там", а са всъщност нещо, което разрушава коя да е научна теория, и при това я разрушава напълно...
Погледнато през очите на автора, това, което ние сега наричаме "квантова механика", започна вече твърде много да прилича на нещо като швейцарско сирене: "там има дупки навсякъде", но не изглежда някой сериозно да е обезпокоен от този факт.
От тази перспектива, "развитието" на физиката през 20-ти век може да бъде видяно като една тъжна история, която някак-си непрекъснато "избира" грешната посока за движение. По-специално, повечето физици са дотолкова свикнали да си мислят за реалността като за нещо, което може да бъде изучавано единствено с помощта на "външни" физически експерименти, че използването на "мисловни" експерименти, или, не дай Боже, на изчислителни експерименти, при това като единствен(!) източник на "физика", им изглежда като откровена лудост.
За тях, ние бихме желали да повторим още веднъж нашата основна теза:
"Ако за едно нещо не може да бъде показано, че то работи, като се използва метода на "ума, молива и хартията", то за това нещо със сигурност може да се каже, че то няма да работи, ако използваме дори и най-съвършената физична лаборатория".
Докато тезисът на Чърч-Тюринг сам по себе си е един достъчно силен аргумент в подкрепа на идеята за "Вселената като клетъчен автомат", с "усилията" на някои физици в последно време (и, особено, на поддръжниците на "квантовото изчисление") даже този аргумент може да не изглежда толкова надежден, колкото той всъщност е.
Но цялостния екстаз от 90-те години по посока разработването на "квантово изчисление" е сега далеч от първоначалните си обещания. Защото през последните пет години твърде незначителен прогрес беше направен. С известно чувство за хумор, някой би могъл да добави, че многото първоначален ентусиазъм сега трудно може да бъде поддържан с купища от теоретични статии, пълни с обещания, и малко, така да се каже, твърде "елементарни" практически резултати, като разделянето на числото 15 на множители 5 по 3.
Докато последното все още може да бъде разглеждано като накякъв "голям научен пробив", истината е, че за повечето проблеми, които първоначално изглеждаха решаеми "по-бързо", като се използват квантови компютри, сега може да кажем, че принадлежат към същите класове от проблеми, решаеми за същото количество време върху добрите стари конвенционални (т.е. "неквантови") компютри.
Независимо от многото шум, вдиган напоследък от поддръжниците на идеята за квантовото изчисление, класическият тезис на Чърч-Тюринг, според нас, е всъщност в едно доста добро състояние: макар да е вярно, че той се нуждае от някаква ревизия, това не е "ревизия" в смисъл, че всичко следва да бъде изоставено като "ненадеждно", и ние трябва да започнем да си мислим за света като за нещо, което изобщо не се поддава на никакво логически непротиворечиво обяснение.
Феномените на квантовия свят могат да бъдат обяснени по начин, който преполага наличието на по-малко "магия", отколкото текущо се предполага. Докато за някого това може да изглежда "разочароващо" и не толкова "вдъхновяващо", от строго научна гледна точка ние определено би трябвало да бъдем доволни да знаем истината, каквато и да е тя.
За жалост, ние можем да добавим, има една специална категория от добре образовани опоненти, които имат склонността да отхвърлят всичко, което е свързано по някакъв начин с предположения за "дискретност" и "детерминизъм" във физиката и науката като цяло; те просто гледат на такава идея като на "абсурд" или "ерес".
Всъщност, ние не молим за тяхното одобрение: твърде вероятно, нашите аргументи от областта на теоретичната информатика могат да им изглеждат твърде абстрактни, и те би следвало да бъдат пренасочени да прочетат още веднъж класическите работи на Фредкин [Fre90] или наскоро публикуваната книга на Волфрам [Wol02]. За тях, един по-илюстративен подход като този на Волфрам, който включва безчислен брой примери, вариращи от всичко, като се започне от шарките върху накои морски черупки и се свърши с политиката, или се демострират красиви клетъчно-автоматни симулации на снежинки и се завърши с разсъждения за комуникации с извънземни светове — за тях подобен подход може да се окаже по-добър.
Все пак, за този тип хора с подобен начин на разсъждение, твърде малко би могло да бъде направено: ние можем само да се надяваме, че след като изложим някои резултати от нашата теория за "Цифровата физика" в следващите статии от тази поредица [Pet02], всичко изложено дотук ще престане да изглежда само като "фантазия" и ще започне да придобива очертанията на една логически непротиворечива и красива теория — такава, каквато ние я виждаме.
Нашата надежда е също, че новото поколение учени, което е било родено през компютърната ера, няма да бъде толкова здраво свързано с този вид "непрекъсната" математика и физика така, както учените от по-старата генерация, за съжаление, са.
Както Едуард Фредкин остроумно вметна веднъж:
"Проблемът в преподаването на Цифовата физика не се състои в това колко много трябва да бъде научено, а по-скоро в това, колко много трябва да бъде забравено."
И също:
"Има удивително малко физици, които изобщо нещо разбират от теоретична информатика."
Все пак, другото злополучно нещо е, че огромната мощ, "заключена" в едно наистина изключително по своя характер твърдение като "Вселената е клетъчен автомат", не е била никога осъзната и докрай използвана от своя автор (Ед Фредкин) [FP97].
Последното приоткрехва вратата за нашата следваща статия [Pet02a3]. Но това е друга история...
От всички статии от настоящата "Серия..." [Pet02] настоящата е единствената, в която ние се опитваме, по един или друг начин, да убедим читателя, че нашата Вселена е наистина клетъчен автомат. В следващите наши статии ние ще се концентрираме не върху това да привеждаме още аргументи в подкрепа на това твърдение (тезиса на Цузе-Фредкин), а по-скоро върху нашата обща теория, а именно:
"Ако Вселената е наистина KA, то какъв КА (точно) би трябвало да бъде Тя?"
Защото, в крайна сметка, тезисът на Цузе-Фредкин е това, което той казва, че е: един тезис, т.е. математически недоказуемо твърдение, което просто трябва или да бъде прието за вярно, или да бъде отхвърлено като невярно.
Основна теза на настоящата работа се състои в това, че Алън Тюринг всъщност почти е успял да се досети за цялата работа още някъде в средата на тридесетте години (1935-36 г.): неговата универсална машина на Тюринг е, фактичеки — ни повече, ни по-малко — (донякъде примитивна форма на) универсален едномерен клетъчен автомат.
Все пак, за да започнем да "виждаме" пълната картина на нещата, ще трябва да разширим модела в три измерения:
Вселената е наистина универсален клетъчен автомат, но тримерен универсален КА (така, както твърди представения тук тезис на Фредкин-Петров), а не едномерен универсален КА или универсална машина на Тюринг (така, както би следвало от тезиса на Чърч-Тюринг).
Иначе, за автора на настоящата статия верността на тезиса на Цузе-Фредкин, че Вселената е клетъчен автомат, не е някъв повод за дискусия; това е просто факт.
Математически непроверим факт, но все пак... факт.
* Тази статия е част от [Pet02].
1 За да бъдем докрай точни: Тезисът на Цузе-Фредкин плюс едно метафизично твърдение, известно като "Бръснач на Окам". Обаче, "Бръсначът на Окам" е често смятан за толкова "очевиден" метафизичен принцип, че ние даже можем да го "пренебрегнем", твърдейки, че последния е просто "мълчаливо вграден" в самите основи на която и да е наука.
2 Историческите бележки по-долу са взети в голямата си част от Уикипедия (Wikipedia), безплатна Интернет енциклопедия — един отличен онлайн източник за математическа, физическа, информатическа и друга сродна информация. В частност, вижте:
http://www.wikipedia.com/wiki/The+Church-Turing+thesis&action=edit
за едно по-задълбочено разглеждане на историческия фон в появата и развитието на идеята за Тезиса на Чърч-Тюринг.
3 Недетерминистична Машина на Тюринг е модел на изчисление, базиран на Машина на Тюринг, която използва вероятностни, а не детерминистични функции в своята "таблица на преход", за да определи следващото си "вътрешно състояние" (състояние на регистъра).
4 Всъщност, MWI, суперстрингове, и различни теории от този род, макар и доста "модни" в наше време, не са дори примери за "строги математически теории" (говорейки стриктно), а повече се явяват като предложения за теории. Нашето мнение обаче е, че такива физико-подобни фантазии би следвало да бъдат ясно разграничвани от нещо, което наистина има добре дефиниран математически апарат зад себе си.
5 Почти единственото, което можем да направим за някой, който вярва в противното, е да му препоръчаме да започне да пише повече компютърни програми. Наистина, практиката на компютърното програмиране помага изключително много човек да "премести" своята гледна точка, или "начин за възприемане на реалността", от единия възможен поглед върху нещата към другия.
6 Така, както прави Фредкиновата "Цифрова Механика" — за сравнение вж. [Fre90].
7 Или, най-малкото, едно директно следствие би било, че съществува някаква TOE, която представя нашата Вселена така, сякаш тя е фундаментално едномерна в пространството.
8 Така, както ние направихме това за парадокса на Айнщайн-Подолски-Розен в [Pet02m].
9 Всъщност, това "просто" твърдение е далеч от очевидно; то ще бъде изследвано по-късно в [Pet02j].
10 За автора на тази статия всеки, който сериозно вярва, че "има някакъв шанс за квантовата механика да демонстрира математически функции, които не (?) са изчислими върху универсална машина на Тюринг", е просто автор на научно-фантастична литература. В този смисъл, нашата позиция е, че добрият стар тезис на Чърч-Тюринг е все още в много добро състояние, независимо от неговата почтителна възраст.
11 Заради шегата, бихме могли да добавим, че този "книжен змей" е вероятно направен от една камара физични статии, прибързано провъзгласили "ерата" на новото "квантово изчисление" и публикувани в множество иначе авторитетни физични списания от 1985 г. насам.
12 Написанo някъде ок. 370 г. Пр.Хр.. Онлайн версия (на английски език) е достъпна на адрес: http://classics.mit.edu/Plato/parmenides.html
13 Добър онлайн източник за парадоксите на Зенон е [Hug02].
14 Последното е известно като "супер-задача" ("supertask") — за повече информация вж. [Lar99].
[Bel64] Bell, John, "On the Einstein Podolsky Rosen paradox", Physics 1 #3 (1964) 195.
[Chu32] Church, Alonzo, "A Set of Postulates for the Foundation of Logic", Annals of Mathematics, second series, 33 (1932) .
[Chu36a] Church, Alonzo, "An Unsolvable Problem of Elementary Number Theory", American Journal of Mathematics 58 (1936) .
[Chu36b] Church, Alonzo, "A Note on the Entscheidungsproblem", Journal of Symbolic Logic 1 (1936) 40-41.
[CFM02] Conway, John, Edward Fredkin, Norman Margolus, Plamen Petrov, Tommaso Toffoli, et al., private e-mail discussion (2002).
[EPR35] Einstein, A., B. Podolsky and N. Rosen, "Can quantum-mechanical description of physical reality be considered complete?", Physical Review 41 (1935) .
[FP97] Fredkin, Edward and Plamen Petrov, private communications, Brookline, MA (1996, 1997).
[Fre90] Fredkin, Edward, "Digital Mechanics: An Informational Process Based on Reversible Universal CA'', Physica D 45 (1990) .
Онлайн версия: http://digitalphilosophy.org/dm_paper.htm
[Fre01] Fredkin, Edward, Introduction to Digital Philosophy, online document (2001).
Вж. глава 14, забележка 1, на адрес: http://digitalphilosophy.org
[Gar71] Martin Gardner, "Mathematical Games: On Cellular Automata, Self-Reproduction, the Garden of Eden, and the Game 'Life' ", Scientific American 224 (February 1971) .
[Goe31] Gödel, Kurt, "Uber formal unentseheidbare Satze der Principia Mathematica und verwandter Systeme I" ("On formally undecidable propositions of Principia Mathematica and related systems I"), Monatshefte fur Mathematik und Physik 38 (1931) . Translated in: van Heijenoort, "From Frege to Godel", Harvard University Press (1971).
Онлайн версия: http://www.ddc.net/ygg/etext/godel/
[Goe34] Godel, Kurt, On Undecidable Propositions of Formal Mathematical Systems (1934), Lecture notes taken by Kleene and Rosser at the Institute for Advanced Study. Препубликувано също и в: Davis, M. (ed.), "The Undecidable", New York: Raven (1965).
[Gut96] Frequently Asked Questions About Cellular Automata (CA FAQ), edited by Howard Gutowitz (1996). Вж. "Is there is universal 1D CA?" ("Съществува ли едномерен универсален клетъчен автомат").
Достъпно онлайн на адрес: http://web.archive.org/web/20010405063359/http://alife.santafe.edu/alife/topics/cas/ca-faq/properties/properties.html#SECTION00029000000000000000
[Hea21] Heath, Thomas, A History of Greek Mathematics 1, Clarendon Press, Oxford, (1921). Reprint: Dover Publ., New York (1981).
[Her32] Herbrand, Jacques, "Sur la non-contradiction de l'arithmetique", Journal fur die reine und angewandte Mathematik 166 (1932) 1-8.
[Hug02] Huggett, Nick, "Zeno's Paradoxes". In: Stanford Encyclopedia of Philosophy, edited by Edward Zalta (2002).
Онлайн версия: http://plato.stanford.edu/entries/paradox-zeno/
[KQS85] Kennedy, J. W., Quintas, L. V. and Syslo, M. M., "The Theorem on Planar Graphs", Historia Math. 12 (1985) .
[Kle35] Kleene, Stephen, "A Theory of Positive Integers in Formal Logic", American Journal of Mathematics 57 (1935) , .
[Kle36] Kleene, Stephen, "Lambda-Definability and Recursiveness", Duke Mathematical Journal 2 (1936) .
[Kur30] Kuratowski, C. "Sur le problème des courbes gauches en topologie", Fund. Math. 15 (1930) .
[Lar99] Laraudogoitia, Jon, "Supertasks". In: Stanford Encyclopedia of Philosophy, edited by Edward Zalta (1999).
Онлайн версия: http://plato.stanford.edu/entries/spacetime-supertasks/
[Mar54] Марков, А., "Теория алгоритмов", Труды МИАН СССР, 42, Издателство АН, Москва (1954). Превод на английски език: American Mathematical Society Translations, series 2, 15 (1960) 1-14.
[Pea96] Pearson, David, "Programming a crystal-lattice computer", Proceedings of the Fourth Workshop on Physics and Computation. In: T. Toffoli, M. Biafore, and J. Leão (ed.), PhysComp96, New England Complex Systems Institute (1996) .
Достъпно онлайн в InterJournal: http://www.interjournal.org/cgi-bin/manuscript_abstract.cgi?540078425
[Pet02] Petrov, Plamen, Series of Brief Articles about Digital Physics (DP), in preparation. За последна информация, вж. https://digitalphysics.org/Publications/Petrov/DPSeries/
[Pet02a1] Petrov, Plamen, "Church-Turing Thesis is Almost Equivalent to Zuse-Fredkin thesis (An Argument in Favor of Zuse-Fredkin thesis)", draft (2002). Тази статия е част от [Pet02].
Достъпно онлайн: https://digitalphysics.org/Publications/Petrov/Pet02a1/Pet02a1.htm
[Pet02a3] Petrov, Plamen, "Zuse-Fredkin thesis is the Ultimate Form of Church-Turing Thesis", in preparation.
[Pet02b] Petrov, Plamen, "The Game (Introduction to Digital Physics)", InterJournal of Complex Systems, submitted, 604 (2002). Тази статия е част от [Pet02].
Онлайн версия: https://digitalphysics.org/Publications/Petrov/Pet02b/Pet02b.htm
[Pet02f] Petrov, Plamen, "Synchronization without Synchronization", draft (2002). Тази статия е част от [Pet02].
Онлайн версия: https://digitalphysics.org/Publications/Petrov/Pet02f/Pet02f.htm
[Pet02g] Petrov, Plamen, "What is Emulation?", in preparation.
[Pet02i] Petrov, Plamen, "Goedel's Incompleteness Theorems and How Digital Physics Interprets Them", in preparation.
[Pet02j] Petrov, Plamen, "Petrov's Hypothesis is (almost) a Theorem", in preparation.
[Pet02m] Petrov, Plamen "Bell's Theorem is Invalid for Cellular Automata, or Demonstrating EPR effects on a One-Dimensional (Non-Quantum) CA", InterJournal of Complex Systems, submitted, 612 (2002). Тази статия е част от [Pet02].
Онлайн версия: https://digitalphysics.org/Publications/Petrov/Pet02m/Pet02m.htm
[Pop34] Popper, Karl, Logik der Forschung, J.C.B.Mohr, Tubingen (1934). Превод на английски език: "The logic of scientific discovery", New York: Basic Books (1959).
[Sch35] Schrödinger, Erwin, "Die gegenwartige Situation in der Quantenmechanik", Naturwissenschaften, 23 (1935) , , . Превод на английски език: John D. Trimmer, Proceedings of the American Philosophical Society 124 (1980) . Препечатано също в: "Quantum Theory and Measurement" (1983) 152.
[Tur36] Turing, Alan, "On Computable Numbers, With an Application to the Entscheidungsproblem", Proceedings of the London Mathematical Society, Series 2, Volume 42 (1936-37) ; Corrections, Ibid., vol. 43 (1937) . Препечатано в: M. David (ed.), "The Undecidable", Hewlett, NY: Raven Press (1965).
Онлайн версия: http://www.abelard.org/turpap2/tp2-ie.asp
[Wol02] Wolfram, Stephen, A New Kind of Science, Wolfram Media, Inc., Champaign IL (2002), 1192 pp.
За повече информация в Интернет: http://www.wolframscience.com
[Wri88a] Wright, Robert, "Did the Universe Just Happen?", Atlantic Monthly (April 1988) 29-44. Превод на български: "Компютър ли е Вселената?", сп."Спектър", бр. 66 (1989) стр. 42-51.
Онлайн версия (на английски език): https://digitalphysics.org/Publications/Wri88a/html/
Онлайн версия (на български език): https://digitalphysics.org/Publications/Wri88a-Bul/html/
[Wri88b] Wright, Robert, Three Scientists and Their Gods: Looking for Meaning in an Age of Information, Times Books (1988). Вж. "Част първа: Едуард Фредкин" ("Part One: Edward Fredkin").
[Zus36] Zuse, Konrad, "Verfahren zur selbsttätigen Durchführung von Rechnungen mit Hilfe von Rechenmaschinen", Patentanmeldung Z 23 139 / GMD Nr. 005/021 (1936).
[Zus67] Zuse, Konrad, "Rechnender Raum", Elektronische Datenverarbeitung 8 (1967) .
Онлайн версия:
[Zus69] Zuse, Konrad, "Rechnender Raum", Schriften zur Datenverarbeitung, Band 1, Friedrich Vieweg & Sohn, Braunschweig (1969).